Meeting No.11: BigBite Optics Calibration #4
New method for determination of the matrix elements

I am trying to write a more accurate code for the determination of the matrix elements.
The general idea is to determine the delta matrix element by looking how delta depends on Fp.Th
for different values of Fp.x (or vice versa). Up until now, I selected few (approx. 8) different momentum
points for each setting of Fp.x. I did this procedure for 7 different Fp.x.
Now I have decided to use different technique. First I determined the area on the FP, that is
covered by Elastic runs. From now on, I will limit my analysis only to events that originate
from this area. I will neglect the rest of the events (at least for now), because
I can not determine optics precisely enough for those events, using the polynomial interpolation.
No that I know the limits, I divided the focal plane into 20 (0.035m wide) slices in FP.x. For each
of these slices I then tried to determine, how delta depends on FP.th. This time I did not
use discrete points but wrote my own version of profiling algorithm. It determines the mean value of
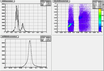
delta and its sigma for each bin in Fp.th. This way I was able to determine the functional dependence delta(th) more precisely. Results of this algorithm are shown in figures below. For the fitting function I used 3rd order polynomials.




















Here is a pdf made from the Mathematica file, with all the fits and values that we need
for the determination of the delta matrix element:
DeltaCalibration.pdf
dE/E vs. BB-momentum:
I have also tried to write a code, that would determine the approximate value of the BB momentum,
using the dE/E plots. In order to do so I used Bethe-Bloch formula to determine what are the
energy losses of the protons with different momenta in our scintillation planes. Once I knew
both punch-through points and had the shape if the curve, I had to rescale it so that my
theoretically determined curve would "sit" on the data. By doing this I also had to consider, that
light output of the plastic scintillator is not proportional to the energy-losses but obeys the Birks
formula. Therefore I had to "guess" five parameters in order to fit my curve to the data: two offsets, two scaling factors and one Birks constant.
Unfortunately this theoretical curve, that I found describes only mean energy losses. However,
real data are smeared around this value, due to various reasons: different flight-paths through
scintillator, energy straggling, etc. Therefore I had to find a way to assign momentum to the
points that do not lie on the mean-energy-loss curve. I made the following approximation.
I have calculated the position of the protons in the dE/E plane for momenta raging from 50MeV
to 1000MeV in steps of 1MeV. I than chose these theoretical values as my reference points. For every measured point in the dE/E plane I determined the distance to each of these reference points and then assigned
to it the momentum of the closest point. This procedure seems to be working pretty well every where
except near the punch through point. There we get some strange results, due to the sharp end
of the curve. I still need to find the solution for this problem.


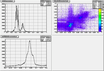


Here is a pdf made from the Mathematica file, that shows how I determined the mean dE/E curve
and how the whole thing works: EnergyLossEdE.pdf
Last Modified: 11/30/09


























