Wonderful World of Pentaquarks: Technical Information
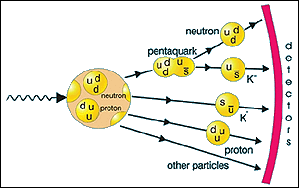
Figure 1: Detection of particles used to reconstruct the pentaquark state.
Dozens or even hundreds of protons and neutrons can be combined together to form the known nuclei of atoms. But when it comes to putting quarks together to form protons, neutrons or other particles, they only come in packages of twos or threes. Or at least so it was thought until recently. For over 30 years, physicists have searched for exotic particles known as pentaquarks, which have a valence structure of four quarks and one antiquark. In the fall of 2002, evidence for a narrow baryon state with an exotic strangeness quantum number — consistent with a pentaquark structure — was presented at the PANIC conference [1]. Since then, many independent experiments have confirmed the existence of this state.
So why is this an exciting discovery? In the simplest terms, it tells us that the number of particles made from quarks is likely to be much more than just the 3-quark baryons and quark-antiquark mesons that are given in the textbooks. Furthermore, it may tell us that there are symmetries present in solutions to non-pertubative QCD that are not evident in the simple quark model. Evidence for new mesons discovered at BaBar, Belle and CLEO also suggest that the simple quark model is not adequate [2] and may require a new paradigm.
Symmetry properties have always played a significant role in describing the spectrum of hadrons, and so it is not surprising that they have had a central role in the recent discovery of pentaquarks. In 1963, Ne'eman and Gell-Mann predicted the existence of the Ω- consisting of three strange quarks based the SU(3) group theory for quarks [5,6]. The discovery of the Ω- at Brookhaven [7] three years later was a startling confirmation of the new quark model. At the heart of this model is group theory, with the lowest mass spin 1/2 baryons organized into an octet group and the spin 3/2 baryons (at higher mass) organized into a decuplet group [3]. The prediction of pentaquarks and subsequent experimental verification of their existence has renewed the interest in how quarks are bound inside hadrons.
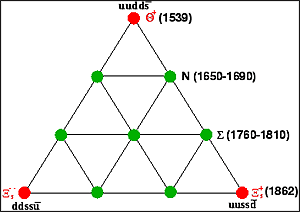
Figure 2: Pentaquarks are expected to be members of an anti-decuplet group of particles. This group is represented by plotting the strangeness of the particles vs. the third component of isospin. The three corners of the triangle (in red) are exotic, which means that their quantum numbers require more than three quarks. The masses of the states are indicated in parenthesis after setting the mass of the Θ+ and Ξ5-- to the observed experimental values [9].
Symmetry properties also led to the theoretical prediction of the pentaquark. While baryons are made out of three quarks (qqq), the pentaquark has a qqqqq configuration, and hence will form a different theoretical group structure. The lowest-mass pentaquark structure was known [4] to be an anti-decuplet, which is triangular like the decuplet but pointing up instead of down (see Figure 2). This anti-decuplet is predicted within the chiral soliton model as an excitation of the usual low mass octet and decuplet families. The symmetries of the model predicted, with input from some experimental masses, the mass of a pentaquark at 1.53 GeV and a decay width of only 0.015 GeV or less [9]. The quark content of this particle, called the Θ+, is two up quarks, two down quarks and one anti-strange quark (ududs). The anti-strange quark cannot annihilate with the other four quarks, and hence this particle cannot be described by just three quarks.
The Θ+ can be identified experimentally by its unique strangeness quantum number. The anti-strange quark gives the Θ+ a strangeness number of S=+1, whereas conventional three-quark baryons (like the Λ with uds quarks) have the opposite strangeness S=-1. Also, the Θ+ has baryon number 1 since each quark has baryon number +1/3 and the antiquark has baryon number -1/3. The well-established principles of baryon number and strangeness conservation allow experiments to pick out the mass spectra for S=+1 final states, where no three-quark baryon can be made. A narrow peak on top of a broad non-resonant background signals the presence of a pentaquark resonance.

