Theory Center Research Highlights
Many-Body Nuclear Physics and the Nuclear Medium
Temperature-density phase diagram for nuclear matter and quark matter. The radius of the nucleon is chosen to be 0.6 fm. H denotes the phase of nuclear matter, M the mixed phase, and C and D the quark phases.
"Phase transition from hadronic matter to quark matter"
P. Wang, A. W. Thomas, A. G. Williams
Phys. Rev. C 75, 045202 (2007)
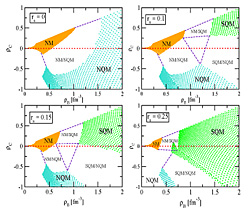
We study the phase transition from nuclear matter to quark matter. The SU(3) quark mean field model with the nucleon exclusive volume effects is applied to obtain the equations of state for nuclear matter. The color superconductivity quark matter is discussed in the NJL model. At low temperature, when the density is about 2.5 - 5 times the saturation density of symmetric nuclear matter, a phase transition from nuclear matter to color superconductivity quark matter takes place. At zero density, when the temperature is larger than about 148 MeV, the quark phase appears. The phase transition from nuclear matter to quark matter is always of the first order, while the transition between color superconductivity quark matter and normal quark matter is of second order.
Ratios of in-medium to free hadron masses as a function of density ρB (normalized to the nuclear matter density ρ0): (top panel) baryons, (bottom panel) mesons.
"Nucleon and hadron structure changes in the nuclear medium and impact on
observables"
K. Saito, K. Tsushima, A. W. Thomas
Prog. Part. Nucl. Phys. 58, 1 (2007)
We have studied the effect of hadron structure changes in a nuclear medium using the quark-meson coupling (QMC) model, in particular the properties of finite nuclei, hypernuclei, a variation of the nucleon form factors in nuclear matter, η-, ω- and D-meson nucleus bound states, subthreshold K production in heavy ion collisions, D and anti-D meson production in antiproton-nucleus collisions, and J/Ψ suppression. Our investigation indicates that the traditional nuclear/hadronic physics approach may have its limitations, and suggests the need to introduce subhadronic degrees of freedom even at normal nuclear matter density.
"The phases of isospin asymmetric matter in the two flavor NJL model"
S. Lawley, W. Bentz, A.W. Thomas
Phys. Lett. B 632, 495 (2006)
We investigate the phase diagram of isospin asymmetric matter at T=0 in the two flavor Nambu-Jona-Lasinio model. Our approach describes the single nucleon as a confined quark-diquark state, the saturation properties of nuclear matter at normal densities, and the phase transition to normal or color superconducting quark matter at higher densities. The resulting equation of state of charge neutral matter is discussed.
The masses of hadronic stars versus their radii. The dotted, dashed and solid curves represent pure neutron stars, nonstrange, and strange hadronic stars with beta-equilibrium, respectively.
"Neutron stars and strange stars in the chiral SU(3) quark mean field
model"
P. Wang, S. Lawley, D. B. Leinweber, A. W. Thomas, A. G. Williams
Phys. Rev. C 72, 045801 (2005)
We have investigated neutron stars and strange hadronic stars in the chiral SU(3) quark mean field model. The equations of state for pure neutron matter, nonstrange, and strange hadronic matter in beta-equilibrium, including Λ, Σ and Ξ hyperons are discussed. The masses and radii of these kinds of stars are obtained. For a pure neutron star, the maximum mass is about 1.8 times of solar mass Msun, while for a strange (nonstrange) hadronic star in beta-equilibrium, the maximum mass is around 1.45 Msun (1.7 Msun). The typical radii of pure neutron stars and strange hadronic stars are about 11.5-13.0 km and 11.5-12.5 km, respectively. Our results are reasonable compared with the astrophysical observations where the six known neutron stars have masses in the narrow range 1.28-1.44 Msun.