Nuclear Physics Archive
Experiment
Strong Coupling Constant at Low Q2
The strength of the strong force is set by the value of its coupling αs. At small distances, much smaller than a fermi (1 fermi = 10-15m, about the size of a proton), αs is small and the strong force can be studied with the standard methods of perturbation theory. This discovery by David J. Gross, H. David Politzer and Frank Wilczek was acknowledged by the 2004 Nobel Prize in Physics. However, at large distances (greater than about a half fermi) the strength of the force becomes large and the perturbative calculations predict that αs becomes infinite. On the other hand, it is not clear if this result can be trusted, since perturbative calculations work only for small αs.
Several nonperturbative theoretical approaches have conjectured that at large distances, the coupling should "freeze" at a constant value. (A few others have suggested that it may even vanish.) No direct experimental tests of these speculations have been made until recently, however. In the nonperturbative domain, one can define "effective" strong couplings [Ref. 1], which absorb all nonperturbative effects (as well as higher-order perturbative effects) in their definition. Because nonperturbative effects depend on the studied physical process, effective couplings are process dependent.
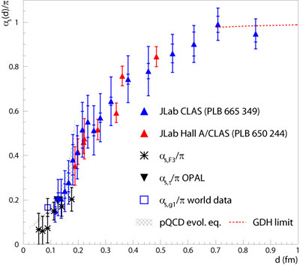
The effective strong coupling extracted from JLab structure function data, as well as from other processes, is shown in Figure 1 as a function of the distance d [Ref. 2]. It suggests that α seff obtained from the Bjorken sum rule tends to a constant (or "freezes") at large d. Such behavior is an essential ingredient in applying the AdS/CFT (Anti de Sitter Space/Conformal Field Theory) correspondence [Ref. 3] to the strong force, since the lack of Q2-dependence of α seff means that the theory of the strong force is a conformal field theory. The application of this correspondence, established in the context of superstring theories, opens promising opportunities for calculations in the nonperturbative regime of the strong force [Ref. 4]
References:
[1] G. Grunberg, Phys. Lett. B 95 (1980) 70; S. J. Brodsky, H. J. Lu, Phys. Rev. D 51 (1995) 365
[2] A. Deur, V. Burkert, J.P. Chen and W. Korsch, Phys. Lett. B 650 (2007) 244; Phys. Lett. B 665 (2008) 349
[3] J. Maldacena, Adv. Theor. Math. Phys 2 231 (1998), see also Scientific American Nov. 2005
[4] S. J. Brodsky and G. de Teramond, Phys. Rev. Lett. 94 (2005) 201601; Phys. Rev. Lett. 96 (2006) 201601
The Quark-Meson Coupling Model
The Quark-Meson Coupling (QMC) model, a theory which takes the radical step of incorporating self-consistent changes in the quark structure of a nucleon when it is bound in matter, has been transformed into a theory of quasi-nucleons interacting through many-body forces. This adjustment allows the QMC model to be related to the time-honored descriptions of the nucleus where nucleon structure was supposed to play no role. Of course, in experiments conducted at very high energies, it is customary to see the nucleus as a collection of quarks interacting via the exchange of gluons. At lower energies, where the spatial resolution is lower, one is apt to view the nucleus in terms of nucleons interacting via the exchange of mesons.
Actually, even in the lower energy range, one should keep the quarks in mind, because their motion inside a nucleon may change when it resides in a nucleus. That is, a nucleon is one thing when on its own and another thing when inside a nucleus, in which case it becomes a "quasi-nucleon". The QMC model takes this dichotomy into account by describing the interactions between a quark in one nucleon with a quark in another nucleon by meson exchange (see illustration at www.aip.org/png/2004/220.htm). The quarks in that nucleon are in turn interacting with the quarks in another and so on. The nucleus is now seen as quasi-nucleons interacting through forces which involve 2, 3, or even 4 bodies. The necessity of such many-body forces was empirically known from traditional nuclear physics, and the merit of the QMC model is that it explains their origin and predicts their intensity. The newer version of the QMC model will enable one to pursue more dramatic impacts of the change of hadron properties in medium, including the modification of weak and electromagnetic form factors.
References:
P. A. M. Guichon and A. W. Thomas, Phys. Rev. Lett. 93 (2004) 132502
K. Saito, K. Tsushima and A. W. Thomas, Prog. Part. Nucl. Phys. 58 (2007) 1
Quark-Hadron Duality
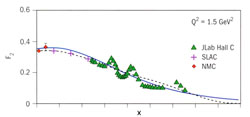
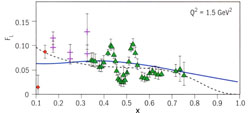
Results of the JLab experiments are shown for the F2 (top) and FL (bottom) structure functions, which describe different aspects of proton structure. Data from previous CERN (NMC) and SLAC experiments are also indicated. The peaks in the JLab data reflect scattering off a composite hadron, whereas the curves reflect scattering off point-like quarks in relative isolation.
Some three decades after the inception of Quantum Chromodynamics (QCD) as the accepted theory for strong interactions, mysteries remain. At high energies, the property of QCD known as asymptotic freedom, in which quarks interact very weakly at short distances, allows for an efficient description of observables in terms of quarks and gluons — or partons. In contrast, at low energies the effects of confinement impose a more efficient description in terms of collective degrees of freedom, the physical mesons and baryons — or hadrons.
Despite this apparent dichotomy, scientists have observed a striking similarity between data measured at high and low energies. This is referred to as "quark-hadron duality." Data accumulated in Hall C at JLab have shown that this quark-hadron duality phenomenon occurs at much lower values of momentum transfer, in more observables, and in far less limited regions of energy than hitherto believed. These studies provide vital clues to the long-standing challenge of QCD to describe the forces at large distances, comparable to the size of hadrons (~1 fm).
References:
W. Melnitchouk, R. Ent and C.E. Keppel, Physics Reports 406 (2005) 127
F. E. Close, Physics World, October 2000, 28
D. Higinbotham, CERN Courier, December 2004
Deuteron Photodisintegration
The structure of the deuteron, the nucleus of the deuterium atom, is of prime importance to nuclear physicists. The deuteron is a bound state of one proton and one neutron, and it is the nucleus most often used in measurements of neutron structure. Studies of the deuteron have helped determine the role of non-nucleonic degrees of freedom in nuclei and the corrections from relativity. A recent series of Jefferson Lab measurements have focused on the role of quarks in the structure of the deuteron. At high-energy and high-momentum transfer, the deuteron is probed at a length scale smaller than the nucleon size and at an energy scale at which the physical picture simplifies — by considering quarks rather than numerous baryon resonances. Measurements of reaction cross sections confirm the approximate scaling behavior expected from the underlying quark structure, while polarization measurements show simple behavior that's in rough agreement with some quark-based calculations.
References:
M. Mirazita et al., Phys. Rev. C 70 (2004) 014005
R. Gilman and F. Gross, J. Phys. G 28 (2002) R37
K. Wijesooriya et al., Phys Rev Lett 86 (2001) 2975
Spin Sum Rules: Transition from Quarks to Nucleons

Q2 evolution of integrals of spin structure functions (left: proton, middle: neutron, right: proton-neutron difference).
Enlarge
The connection between the fundamental quark-gluon and effective hadron descriptions of the strong interaction is a key question of nuclear physics studied at Jefferson Lab. Data obtained with JLab's multi-GeV polarized electron beam and polarized targets in Halls A and B on the spin-dependent g1 and g2 structure functions allow for precise extractions of the Bjorken and Gerasimov-Drell-Hearn integrals for the proton and neutron. These quantities are well suited to study the transition from quark-gluon to hadron degrees of freedom, as they can be compared to both fundamental and effective theory predictions.
The data evolution with Q2 indicates a smooth, yet dramatic, transition. They also show that the effective theory used at small Q2 (chiral perturbation theory) is not as reliable as first expected. At higher Q2, the first order perturbative QCD calculation works down to surprisingly low Q2. This suggests possible cancellations of higher-order effects such as quark-gluon and quark-quark correlations.
(See also entry on Color Polarizabilities)
References:
M. Amarian et al., Phys. Rev. Lett. 89 (2002) 242301
R. Fatemi et al., Phys.Rev.Lett. 91 (2003) 222002
M. Amarian et al., Phys.Rev.Lett. 92 (2004) 022301
A. Deur et al., Phys.Rev.Lett. 93 (2004) 212001
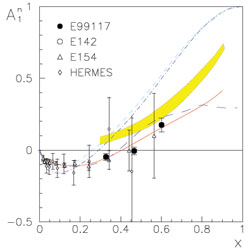
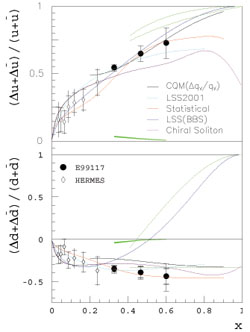
Nucleon Spin Asymmetries: Are Quarks Spinning In the Nucleon as We Expected?
Since the "proton spin crisis" in the late 1980s, it is now accepted that a nucleon's spin comes from not only the spin of its constituent quarks, but also from the quarks' orbital angular momentum (how they move inside the nucleon) and the gluons' angular momentum. However, how these three parts add up to form the nucleon's spin of 1/2 is unclear. Combining recent studies of neutron spin structure with existing proton data, it has been found that quarks may not be spinning in the way physicists expected.
| Do new data on the nucleon spin agree with what we expected in the high x_bj region? Left: Neutron spin asymmetry A1n; Right: Spin directions of quarks inside the nucleon. |
|
References:
X. Zheng et al., Phys. Rev. Lett. 92 (2004) 012004
X. Zheng et al., Phys. Rev. C 70 (2004) 065207
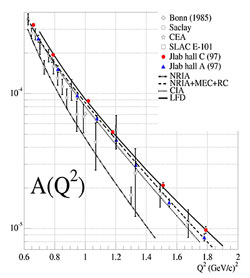
Deuteron Form Factors
The simplest bound system of neutrons and protons is the deuteron, consisting of one proton and one neutron. In the language of the theory of the strong interaction, quantum chromodynamics (QCD), it is made of six valence quarks (3 up and 3 down), plus the quark-gluon sea. In the standard proton-neutron picture, the deuteron's shape is largely determined by the exchange of a pion, which leads to strong, noncentral "tensor" interactions.
Elastic electron scattering at high momentum transfer probes the short distance structure of the deuteron's interior. With ordinary unpolarized scattering, its magnetic and electric distributions can be separated. Adding a polarization observable, such as the recoiling deuteron's "tensor polarization," makes it possible to further separate the electric piece into its charge and quadrupole components. The tensor moment t20 is most sensitive to the deuteron's charge distribution, while the other two moments, t21 and t22, provide important symmetry checks and information about the deuteron's magnetization. The shapes associated with these moments are shown in figure 1.
Two sets of experiments carried out at JLab in the late 1990s push measurements of the deuteron's electromagnetic distributions to the highest momentum transfer presently possible. An unpolarized scattering experiment in Hall A extracted the electric and magnetic structure functions, called A and B, respectively, and the results for A are shown in figure 2. An experiment in Hall C determined the tensor moments t20, t21 and t22. Combining these data has allowed the first determination of the deuteron's charge distribution as it crosses zero and provides very stringent tests of models of the force between two nucleons.
References:
L.C. Alexa, et al., Phys. Rev. Lett. 82 (1999) 1374
D. Abbott, et al., Phys. Rev. Lett. 84 (2000) 5053
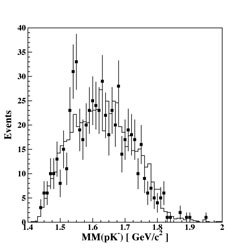
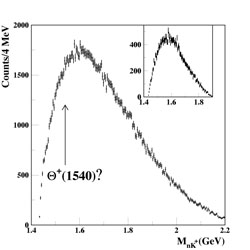
Pentaquark Search
Most known particles have either 3 quarks (baryons) or a quark-antiquark pair (mesons). The pentaquark is defined as a subatomic particle consisting of 4 quarks and one antiquark. If the pentaquark exists, then it would be a breakthrough in our understanding of how quarks can be put together to form composite particles. However, while there were claims by several experiments around the world for a pentaquark (now called the Θ+), newer, higher-statistics experiments put in doubt some of the earlier data claiming evidence for the Θ+. With better exeriments, Jefferson Lab was able to test the hypothesis that earlier experiments might have found evidence for the Θ+ pentaquark. The new data give a null result for the existence of the Θ+. This is an example of the scientific process at work; claims of new particles must be reproducible in experiments with higher statistical precision. Jefferson Lab has played a crucial role in the search for new and exotic types of subatomic particles.
| The results of one experiment using the CLAS detector at Jefferson Lab, called g10, is shown left, where the mass of the (nK+) system is shown. The old results are plotted with points, and the new results are shown as a histogram. It is clear that the peak (excess counts at about 1.54 GeV) in the older data is not reproduced in the new, higher-statistics experiment. Another experiment, also using the CLAS detector and known as g11, tried to replicate the peak seen in an earlier experiment from Germany. The result is shown at right - clearly there is no sharp peak in this mass spectrum. | |
References:
K. Hicks, Prog. Part. Nucl. Phys. 55 (2005) 647
M. Battaglieri et al. (The CLAS Collaboration), Phys. Rev. Lett. 96 (2006) 042001
K. H. Hicks, hep-ex/0510067
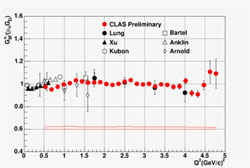
Neutron Magnetic Structure
New data from CLAS in Hall B probe the magnetic structure of the neutron at large momentum transfers, or small distances, with high precision. The magnetic form factor of the neutron, GMn, has been extracted from measurements of the ratio of quasi-elastic, electron-neutron to electron-proton scattering in deuterium over a Q2 range of 0.5-4.8 (GeV/c)2. The CLAS detector enabled the use of a combination of experimental techniques that allowed unprecedented precision to be achieved at Q2 ≥ 1 (GeV/c)2. Preliminary results of these measurements are compared to previous data in the figure at right. These data will provide stringent tests of nucleon structure models and allow for more precise extractions of other nucleon structure information.
Theory
Strangeness Magnetic Moment of the Proton
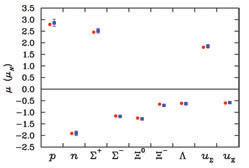
Comparison of experimentally observed magnetic moments (circles) against the theoretical calculation (squares).
Enlarge
A theoretical calculation has produced a prediction of the strange quark contribution to the magnetic moment of the proton, GMP, that is more than 10 times more precise than currently accessible in experiment. This result provides vital information on the hidden-flavor structure of the nucleon. Nucleons are primarily composed of three quarks, two 'up' and one 'down' type quark for a proton, and the reverse for a neutron. Quantum fluctuations can cause brief appearances of any number of quark-antiquark pairs. These pairs can either be the familiar up or down quarks, or possibly a third species of quark, called the strange quark.
These short-lived strange quark pairs certainly contribute to nucleon properties; however, the role the strange quark plays in nucleon structure is controversial and poorly understood. For instance, there have been claims that the strange quark accounts for as much as 20% of the mass of the proton and carries about 10% of the total spin. The present calculation, performed by theorists at Jefferson Lab in collaboration with the CSSM in Adelaide, Australia, has focused on the contribution of strange quarks to the proton's magnetic moment. This calculation has been produced by combining charge symmetry, modern lattice QCD simulation results, and improved chiral extrapolation techniques. This work has produced a prediction for the proton's strange magnetic moment, GMP=-0.046 ± 0.019 nuclear magnetons. In light of the large strange-quark influence on the mass and spin, the latest result is a shockingly small value, representing only half a percent of the total proton magnetic moment.
Previously, there has been large theoretical uncertainty, with model calculations predicting values for GMP over the range -0.4 up to +0.7. The level of precision in the new calculation is unprecedented — greater than 10 times more precise than currently resolved in measurements at MIT-Bates, JLab and Mainz. At the present level of experimental precision, theory and experiment are in agreement. The next generation of experimental programs, such as the 2005 HAPPEx run and the next phase of the G0 experiment at JLab, should provide further insight and a strong test of the theoretical prediction.
As a further check of this calculation, the magnetic moments of the ground state baryon magnetic moments have also been evaluated. The excellent agreement with the experimental values are shown in the figure.
References:
D. B. Leinweber et al., Phys. Rev. Lett. 94 (2005) 212001
D. B. Leinweber, A. W. Thomas and R. D. Young, Phys. Rev. Lett. 92 (2004) 242002
R. D. Young, D. B. Leinweber, A. W. Thomas and S. V. Wright, Phys. Rev. D 66 (2002) 094507
Quark-Hadron Duality and Color Polarizabilities
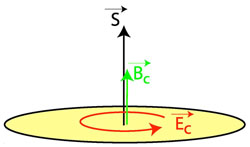
Color polarizabilities: response of the color electric Ec→ and magnetic Bc→ fields in the nucleon when the nucleon is polarized in the direction given by the spin vector S.→
Enlarge
Within the theoretical framework of the operator product expansion, the moments, or integrals over Bjorken-x, of structure functions can be expanded in inverse powers of the momentum scale Q2. The leading term in the expansion corresponds to scattering from free quarks and is responsible for the scaling of the structure functions. The higher order terms involve mixed quark-gluon operators and contain information on long-range correlations between partons, which are related to quark confinement. Quark-hadron duality (equivalence of quark and hadron descriptions of structure function moments) occurs when the higher-order interaction terms are small.
An example of a quantity which reflects such quark-gluon interactions that was extracted recently from moments of the spin dependent structure functions of the nucleon is the "color polarizability." This describes how the color electric and magnetic fields respond when the nucleon is polarized. The results indicate small but positive color electric polarizabilities for both the proton and neutron, but a negative magnetic polarizability for the proton, and one consistent with zero for the neutron. The negative value for the proton magnetic polarizability suggests that, on average, the induced color magnetic field in a proton is oriented in a direction opposite to that of its spin.
Also see Quark-Hadron Duality entry.
References:
M. Osipenko et al., Phys. Lett. B 609 (2005) 259
Z. -E. Meziani et al., Phys. Lett. B 613 (2005) 148
W. Melnitchouk, R. Ent and C.E. Keppel, Physics Reports 406 (2005) 127
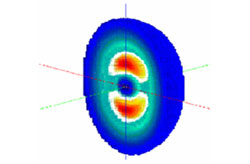
Generalized Parton Distributions: 3D Quark/Gluon Imaging of the Nucleon
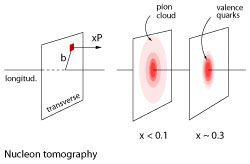
Nucleon tomography.
Enlarge
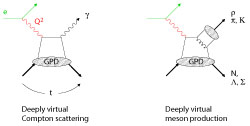
Deeply virtual Compton scattering (left), and deeply virtual meson production (right)
Enlarge
Generalized parton distributions (GPDs) unify the concepts of the nucleon elastic form factors (measured in elastic eN scattering) and parton distributions (measured in inclusive deep-inelastic eN scattering). GPDs describe the form factors for the emission and absorption of a quark/gluon by a fast-moving nucleon, depending on the quark's longitudinal momentum fraction, and the invariant momentum transfer to the nucleon, t. Their Fourier transform with respect to t describes the spatial distribution of quarks in the transverse plane and provides us with a 3D image of the quark and gluon structure of the nucleon in QCD ("nucleon tomography"). This new representation provides a natural framework for describing effects of quark polarization and orbital motion (transverse momentum) in hard scattering processes and offers unprecedented possibilities to visualize the nucleon as an extended object. It also plays an important role in describing high-energy NN collisions with hard processes, such as Higgs boson production at the LHC.
GPDs can be probed in exclusive eN scattering processes, such as deeply virtual Compton scattering (DVCS) and meson production. At large momentum transfer, Q2 >> 1 GeV2, the production process happens in the reaction of the virtual photon with a single quark ("factorization"). The study of these processes and the extraction of the GPDs are one of the prime objectives of the 12 GeV Upgrade of CEBAF. Measurements of DVCS at 6 GeV indicate the applicability of the GPD-based description. Researchers at the JLab Theory Center develop the methods for the analysis of these processes, construct phenomenological models for the GPDs, and relate the information contained in the GPDs to that obtained from other nucleon observables.
References:
A. V. Belitsky and A. V. Radyushkin, Phys. Rept. 418 (2005) 1
M. Guidal, M. V. Polyakov, A. V. Radyushkin and M. Vanderhaeghen, Phys. Rev. D 72 (2005) 054013
L. Frankfurt, M. Strikman and C. Weiss, Ann. Rev. Nucl. Part. Sci. 55 (2005) 403
Few-Nucleon Systems in Chiral Effective Field Theory
Determining the nature of the interaction between nucleons is crucial for understanding nuclear reactions and the properties of nuclei. According to quantum chromodynamics (QCD), the nuclear force is a residual color force between the color-charge neutral hadrons. A direct derivation of the nuclear force from QCD is not yet possible due to its nonperturbative nature in the low-energy regime. Chiral effective field theory (EFT) provides a systematic and model-independent framework to study the properties of hadronic systems. It relies on the chiral symmetry of QCD that governs low-energy hadron dynamics. In the Goldstone boson and single-baryon sectors, this method allows the determination of the scattering amplitude based on the perturbative expansion in powers of the low external momenta and about the chiral limit, the so-called chiral expansion. As shown by Weinberg in the early 1990s, it can also be applied to derive nuclear forces and current operators which may then be used as input in few- and many-body calculations.
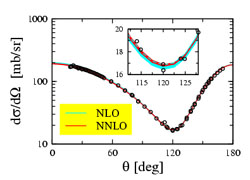
In the past few years, the two-nucleon system has been studied extensively in the framework of chiral EFT. The most advanced analyses at next-to-next-to-next-to-leading order (N3LO) in the chiral expansion demonstrate the ability of the novel chiral forces to provide an accurate description of the data in the low-energy region. The first promising results have also been obtained for three- and more-nucleon systems. The calculations up to next-to-leading order (NLO) are based entirely on the two-nucleon force and, therefore, yield parameter-free results in the case of three and more nucleons. The chiral three-nucleon force first needs to be accounted for at NNLO and depends on two unknown low-energy constants. Having fixed these two parameters from the triton binding energy and the doublet neutron-deuteron scattering length, we applied the resulting parameter-free 3N Hamiltonian to systems with up to 6 nucleons. As a typical example, the figure shows the results for the differential cross section for elastic nucleon-deuteron scattering at Enucl = 10MeV at NLO and NNLO in comparison with the data. The uncertainty estimate is based on the cutoff variation. Further results and applications can be found in a recent review article.
References:
D. R. Entem, R. Machleidt, Phys. Rev. C68 (2003) 041001
E. Epelbaum, W. Glockle, U.-G. Meissner, Nucl. Phys. A747 (2005) 362
E. Epelbaum, nucl-th/0511025