High Momentum Components in the Nucleus

High energy electron scattering from nuclei can provide important information on the wave function of nucleons in the nucleus. With simple assumptions about the reaction mechanism, scaling functions can be deduced that should scale (i.e. become independent of length scale or momentum transfer) and which are directly related to the momentum distribution of nucleons in a nucleus. Several theoretical studies [12,13,14,15] have indicated that such measurements may provide direct access to short range nucleon-nucleon correlations.

The concept of $y$-scaling in electron-nucleus scattering was first introduced by West [16] and by Kawazoe et al. [17]. They showed that in the impulse approximation, if quasielastic scattering from a nucleon in the nucleus was the dominant reaction mechanism, a scaling function $F(y)$ could be extracted from the measured cross section which was related to the momentum distribution of the nucleons in the nucleus. In the simplest approximation the corresponding scaling variable $y$ is the minimum momentum of the struck nucleon along the direction of the virtual photon. The scaling function is defined as the ratio of the measured cross section to the off-shell electron-nucleon cross section multiplied by a kinematic factor:

$$F(y) = {d^2\sigma \over d\Omega d\nu}\frac{1}{(Z \sigma_p + N \sigma_n)} {q \over \sqrt{(M^2 + (y + q)^2)}},$$ (1)

where Z and N are the number of protons and neutrons in the target nucleus, the off-shell cross sections $\sigma_p$ and $\sigma_n$ are taken from $\sigma_{CC1}$ from Ref. [18], $q$ is the three-momentum transfer and M is the mass of the proton. At large $q$, where we can neglect momenta perpendicular to $q$, we can determine $y$ from energy conservation [20]:

$$\nu + M_A = \sqrt{M_N^2 + (y + q)^2} + \sqrt{M_{A-1}^2 + y^2},$$ (2)

where $M_A$ is the mass of the target nucleus and $M_{A-1}$ is the ground state mass of the $A-1$ nucleus. In general, the scaling function depends on both $y$ and $Q^2$, but at sufficiently high momentum transfer the $Q^2$-dependence vanishes, yielding scaling. In this PWIA analysis, the scaling function $F(y)$ can then be directly related to the nucleon momentum distribution:

$$n(k) = -\frac{1}{2 \pi k} \frac{dF(k)}{dk}$$ (3)

This simple impulse approximation picture breaks down when the final-state interactions (FSI) of the struck nucleon with the rest of the nucleus are included. Previous calculations [21,22,23,24,25,26,27,28] suggest that the contributions from final state interactions should vanish at sufficiently high $Q^2$. The scaling function for Fe extracted from experiment E89-008 is shown in Fig. 2 [29]. These data show, for the first time, a clear approach to a scaling limit for heavy nuclei at large $-y$ for $Q^2 > 3$ GeV/c$^2$. This is shown in Fig. 3 for data from E89-008 and SLAC NE3 [1] where the $Q^2$ variation of $F(y)$ for several fixed values of $y$ is shown. Note that the cross section (Fig. 4) varies over many orders of magnitude for the $Q^2$ range shown in the figure.

Figure 2: Scaling function $F(y)$ for Fe from E89-008. The $Q^2$ values are given for Bjorken $x=1$.

Figure 3: Scaling function $F(y)$ vs. $Q^2$ for Fe for fixed values of $y=-0.3, -0.4, -0.5$ (GeV/c). The open points are calculated from the measured cross sections of the SLAC NE3 experiment. The scaling function for each value of $y$ has been multiplied by the factors noted in parentheses.

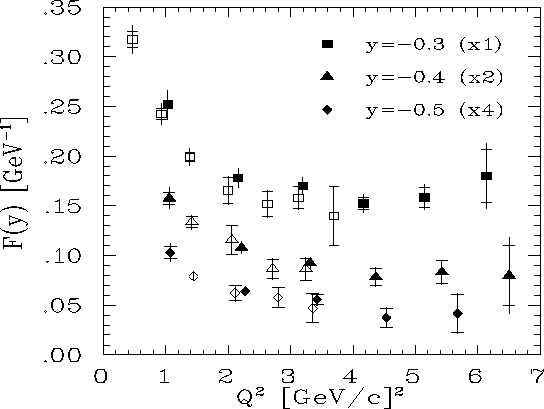While the observation of a scaling limit is suggestive of an approach to the impulse approximation limit, it is not definitive. Even if scaling is observed, that does not insure that the scaling function is directly connected to the momentum distribution (as we will see in the following sections). In addition, several calculations [30,31] have pointed out that while the FSI of a struck nucleon with the mean field of the rest of the nucleus is a rapidly decreasing function of $Q^2$, the FSI of the struck nucleon with a correlated, high-momentum nucleon may show a very weak $Q^2$-dependence. Experimental measurements at higher $Q^2$ are essential in allowing an understanding of the role of FSI in inclusive scattering. As both the large $\vert y\vert$ cross section and the high $Q^2$ FSI discussed above are dominated by short range nucleon-nucleon interactions, improved data at higher $Q^2$ may allow direct access to this interesting many-body phenomenon. The ``holy grail'' of these studies is to correct or eliminate FSI so that by using the impulse approximation, the nuclear spectral function $S(p,E)$ at high values of $p$ and $E$ can be extracted. The region of high $p$ includes the highly interesting regime of short range correlations (SRCs) that are expected to be present within nuclei.

While the PWIA $y$-scaling interpretation of the data promises the possibility to extract the nucleon momentum distribution, the possible contribution of FSIs and questions about the validity of the assumptions of the $y$-scaling analysis have limited the information extracted by this kind of analysis. Clearly, these data do not need to be analyzed in terms of $y$-scaling in order to constrain the high momentum components of the nuclear wave function. However, we will show in the following section that with only a small change to the $y$-scaling model, we extract a scaling function which is fully consistent with the idea that the scaling function is directly connected to the momentum distribution. This would seem to validate the assumptions of the PWIA analysis, and allow a largely model independent connection to be made between the high momentum nucleons and the modified $y$-scaling function.