Nucleon Degrees of Freedom, $F(y)$ Measurements

While the 4 GeV data (and proposed 6 GeV extension) provide additional information on the structure function at large $\xi$, the main focus is the study of the momentum distribution of nucleons in nuclei, and in particular the nature of the high momentum components. The 4 GeV data from E89-008 showed $y$-scaling, with large $Q^2$-dependent scaling violations from final state interactions below $Q^2=3$ GeV$^2$ (Fig. 3). Fig. 6 shows $F(y)$ for deuterium from the 4 GeV run. While the data in the scaling region ($Q^2 > 3$ GeV$^2$) is limited at large $y$, a clear approach to scaling is observed. The solid line is a fit to $F(y)$ of the form suggested in Ref. [34]:

$$F(y) = \frac{A e^{-a^2 y^2}}{\alpha^2 + y^2} + B e^{-b\vert y\vert}.$$ (4)

Figure 6: Scaling function $F(y)$ for deuterium from E89-008, along with fit to data (of form given in Eq. 4).

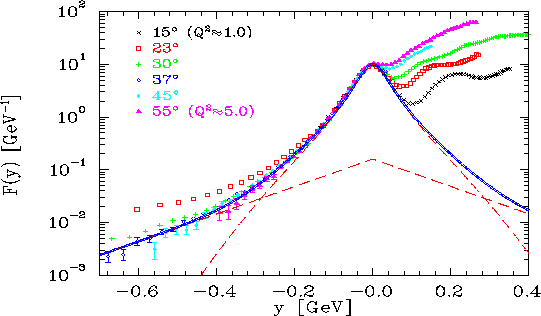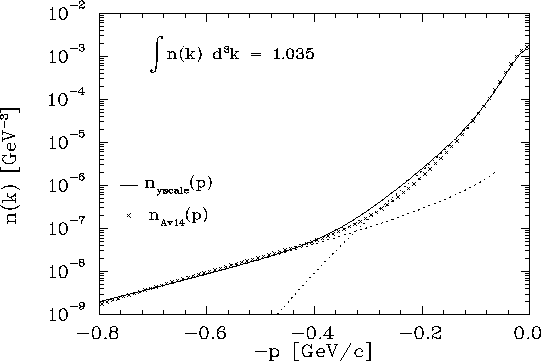
Fig. 7 shows the momentum distribution as extracted (using Eq. 3) from the fit to $F(y)$, along with a calculation using the Argonne v14 NN potential. The agreement is quite good, even at extremely large values of $\vert y\vert$ where $n(k)$ is 4 to 5 orders of magnitude below the peak value. In particular, the slope as well as the normalization on the tail agree quite well with the calculated momentum distribution. The agreement in the tail region, which is dominated by the short range interaction of the nucleons, seems to indicate that the weakly $Q^2$-dependent final state interactions suggested for correlated nucleons do not make a large contribution to the scaling function. The 4 GeV data are of limited quality at the large values of $y$, making it difficult to extract a precise shape and normalization for this tail. Better data on deuterium, with the extended $Q^2$ range possible at higher energy, should allow us to extract more detailed information about the tail of the momentum distribution than we can get from the simple fit used in this analysis. A precise measurement of this region will also allow us to set significant limits on deviations from the momentum distribution due to possible weakly $Q^2$-dependent final state interactions of these strongly interacting (small separation) nucleons.

Figure 7: Momentum distribution, $n(k)$ for deuterium from E89-008 $y$-scaling analysis (solid line), and calculation using the Argonne v14 potential (crosses). The dotted lines indicates the contributions of the exponential tail and the modified gaussian term from the fit to the measured $F(y)$.

While the $y$-scaling analysis of the deuterium data yields results consistent with exact calculations of the momentum distribution, this is not the case for the heavy nuclei. Fig. 2 shows $F(y)$ for iron. While the data show $y$-scaling, the falloff at large $\vert y\vert$ indicates that the high momentum components ( $y \mathrel{\raise.3ex\hbox{$<$}\mkern-14mu \lower0.6ex\hbox{$\sim$}}-0.5$ GeV/c) are much smaller for iron than for deuterium, even though one would expect more high momentum nucleons in the denser nuclei. This is also true for the SLAC $^3$He data, where the extracted $F(y)$ is not consistent with calculations of the $^3$He momentum distribution. In addition, the integral of $F(y)$ should be unity in the $y$-scaling picture, but the normalization of the scaling function for heavy nuclei are $\sim$20-30% low. For the $^3$He data, the normalization of the scaling function has been analyzed in terms of ``swelling'' of the nucleon in the nucleus, and has been used to set upper limit on medium modifications to the nucleon form factors [35]. Extending such an analysis to heavier nuclei, where the normalization is even lower, would lead to a prediction of greater modifications to the nucleon radius. It is not clear that this kind of analysis gives meaningful limits on nucleon medium modifications if there is a more fundamental problem in the relation between $F(y)$ and $n(k)$. Nonetheless, tests of medium modifications from $y$-scaling analyses has been used to set limits on nucleon swelling used to explain the EMC effect.

The rapid falloff of the scaling function at large values of $\vert y\vert$ indicates that there is a failure of some kind in the PWIA scaling analysis. The breakdown for $A > 2$ nuclei comes from the assumption that the residual nucleus remains in an unexcited state (Eq. 2). The NN correlations responsible for much of of the high momentum components are neglected. Clearly the $(A-1)$ spectator nucleus will not be in an unexcited state if one of a pair of very high momentum nucleons is suddenly removed. The scaling violations arising from the assumption of an unexcited final state have been treated in two ways. In some cases, a correction to the scaling function is calculated, and the scaling function that is related directly to the momentum distribution is $f(y) = F(y) - B(y)$, where $F(y)$ is the measured scaling function, and $B(y)$ is the calculated binding correction. A more direct way to take the excitation of the residual nucleus into account is to determine an excitation energy for the residual system based on a modified picture of the interaction that includes the correlations. Rather than having the momentum of the struck nucleon balanced by the residual nucleus, it's momentum is balanced by a single nucleon, and the residual $(A-2)$ nucleus is at rest [36], or has a small recoil momentum [34]. We have performed an analysis of this kind using a modified definition of $y$, based on a simple three-body breakup of the nucleus, where the nucleon struck is assumed to be one of a correlated pair that is moving in the nucleus with a momentum (along the $q$ vector) equal to $K_{CM}$. In the limit where $q$ is much larger than the momenta of the nucleons (and thus the transverse component of these momenta can be ignored), energy conservation gives:

$$\nu + M_A = \sqrt{M_N^2 + (q+k+K_{CM}/2)^2} + \sqrt{M_N^2 + (-k+K_{CM}/2)^2} + \sqrt{M_{A-2}^2 + (-K_{CM})^2}$$ (5)

The scaling variable in this case is $y^* = k + K_{CM}/2$, the total initial momentum of the struck nucleon. Note that for the deuteron, there is no $(A-2)$ residual nucleus and thus no $K_{CM}$, so $y^*$ is just the usual scaling variable $y$. Eq. 5 cannot directly be solved for $y^*$ without a relation between $y^*$ and $K_{CM}$. This is obtained by convolving the center of mass motion of the quasi-deuteron with the relative momentum of the nucleons in the pair (taken to be identical to the real deuteron momentum distribution). This allows us to determine the average $K_{CM}$ for a given value of the initial nucleon momentum.

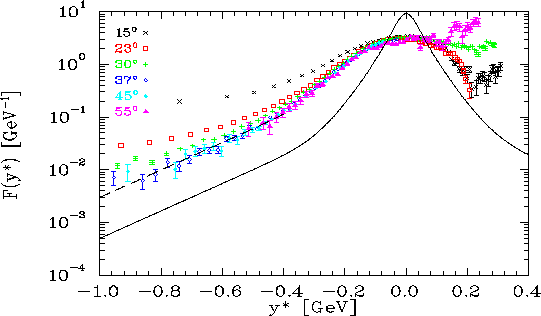
Fig. 8 shows the modified scaling function, $F(y^*)$, along with a fit to to $F_D(y^*)$ (dashed line). In the figure we have made a subtraction of the inelastic contribution which is significant for $y^* \mathrel{\raise.3ex\hbox{$>$}\mkern-14mu \lower0.6ex\hbox{$\sim$}}0$. Note that the behavior at very large negative $y^*$ is very different from the behavior in Fig. 2, and that the data is sensitive to larger values of initial nucleon momentum that one would assume based on the usual $y$-scaling function (probing nuclei with initial momenta of more than 1 GeV/c). However, at these very large $y^*$ values, the uncertainties in the 4 GeV data are large, and the data just barely reach $Q^2$ values where scaling appears to have set in. With data at higher $Q^2$ values in this large $y^*$ region, we should be able to map out the high momentum tail of the nucleon momentum distribution. Also notice that the shape of the scaling function at large negative $y^*$ values is the same as for the deuteron, but is roughly 6 times larger (dashed line), indicating that the high momentum components appear to be well described by two nucleon correlations. This is the same behavior one sees when examining the ratio of the structure functions in the region of $1.3 \mathrel{\raise.3ex\hbox{$<$}\mkern-14mu \lower0.6ex\hbox{$\sim$}}x < 2$, where the ratio is flat and roughly 5 to 6 times higher in heavy nuclei [37,15]. With better data for deuterium at large initial nucleon momenta, this comparison could be much more quantitative, and we could look for signs of high momentum components beyond the two nucleon correlations. In addition, data on $^3$He will allow for direct comparison of high momentum nucleons ($x > 2$) in heavy nuclei to three nucleon correlations.

Figure 8: Scaling function, $F(y^*)$ for Fe from E89-008. The solid line is the fit to $F(y^*)=F(y)$ for deuterium. The dashed line is the tail of the deuteron fit, scaled up by a factor of six.

Of course one does not have to rely on a non-relativistic, impulse approximation scaling analysis to study the momentum distribution and the high momentum components. One can do a complete, relativistic calculation of the cross section, using the full spectral function and including final state interactions. One can also use a relativistic scaling analysis which gives a different scaling variable and connects to light-cone momentum distributions, as suggested in Ref. [6]. The scaling analysis discussed here is intended to give a feel for the coverage and significance of the data, but also to show the success of this simple scaling analysis. This success gives us confidence in the underlying assumptions.

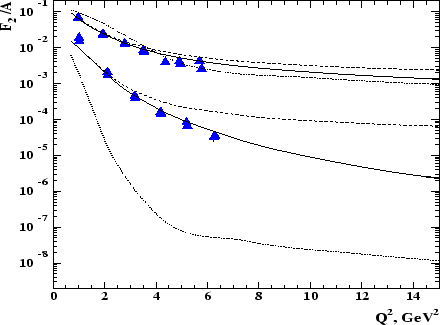
The question of the nature of the short range correlations can also be examined without relying on a $y$-scaling analysis, by directly examining the structure functions. Fig. 9 shows a calculation of the structure function per nucleon for iron, including just two nucleon correlations (solid line - from [38]), and including multinucleon correlations (dotted line - from [13]). The current data clearly indicate that the effect of multinucleon correlations is significantly smaller than estimated in the calculation. The calculation for the two nucleon SRC contributions does not include corrections for the EMC effect, but such a calculation should be available very soon [39]. The inclusion of the EMC effect will lower the calculations somewhat, making it difficult to use this data to set a strong upper limit on multinucleon components. An extension to 6 GeV will allow us to reach $Q^2 \sim 10$ GeV$^2$ at $x = 1.5$, where the calculation predicts very large contribution from multinucleon correlations. In addition, with data on $^2$H, $^3$He, and $^4$He, it should be possible to disentangle the EMC effect from 3N correlations [39,40]. This will allow us to either obtain a clear signal of multinucleon correlations, or set significant limits on their contributions. We can also directly compare the structure function for heavy nuclei to few body nuclei in the region where the structure function is dominated by SRCs. By comparing heavy nuclei to deuterium, we can look for deviations from the two nucleon SRCs, and by comparing to $^3$He where the two nucleon correlations are small for $x > 2$, we can look for signatures of three nucleon correlations. This type of comparison is more direct than comparisons of the extracted momentum distribution from a scaling analysis. In addition, if there are significant final state interactions between correlated nucleons at large $Q^2$ values, these should cancel to first order in these ratios.

Figure 9: Structure function for nucleon for iron from E89-008 compared to calculations without correlations (dotted lines), including two nucleon SRCs (solid lines) and multinucleon SRCs (dashed line). The upper set of data and calculations is for $x=1$, while the lower are for $x = 1.5$.