Strong Coupling Constant at Low Q2
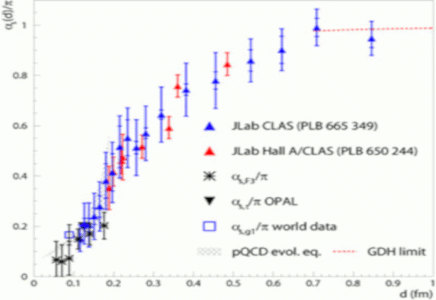
The effective strong coupling αs vs. distance
Additional Links
The strength of the strong force is set by the value of its coupling αs. At small distances, much smaller than a fermi (1 fermi = 10-15m, about the size of a proton), αs is small and the strong force can be studied with the standard methods of perturbation theory. This discovery by David J. Gross, H. David Politzer and Frank Wilczek was acknowledged by the 2004 Nobel Prize in Physics. However, at large distances (greater than about a half fermi) the strength of the force becomes large and the perturbative calculations predict that αs becomes infinite. On the other hand, it is not clear if this result can be trusted, since perturbative calculations work only for small αs.
Several nonperturbative theoretical approaches have conjectured that at large distances, the coupling should "freeze" at a constant value. (A few others have suggested that it may even vanish.) No direct experimental tests of these speculations have been made until recently, however. In the nonperturbative domain, one can define "effective" strong couplings [Ref. 1], which absorb all nonperturbative effects (as well as higher-order perturbative effects) in their definition. Because nonperturbative effects depend on the studied physical process, effective couplings are process dependent.
The effective strong coupling extracted from JLab structure function data, as well as from other processes, is shown in Figure 1 as a function of the distance d [Ref. 2]. It suggests that α seffobtained from the Bjorken sum rule tends to a constant (or "freezes") at large d. Such behavior is an essential ingredient in applying the AdS/CFT (Anti de Sitter Space/Conformal Field Theory) correspondence [Ref. 3] to the strong force, since the lack of Q2-dependence of α seff means that the theory of the strong force is a conformal field theory. The application of this correspondence, established in the context of superstring theories, opens promising opportunities for calculations in the nonperturbative regime of the strong force [Ref. 4]
References:
[1] G. Grunberg, Phys. Lett. B 95 (1980) 70; S. J. Brodsky, H. J. Lu, Phys. Rev. D 51 (1995) 365
[2] A. Deur, V. Burkert, J.P. Chen and W. Korsch, Phys. Lett. B 650 (2007) 244; Phys. Lett. B 665 (2008) 349
[3] J. Maldacena, Adv. Theor. Math. Phys 2 231 (1998), see also Scientific American Nov. 2005
[4] S. J. Brodsky and G. de Teramond, Phys. Rev. Lett. 94 (2005) 201601; Phys. Rev. Lett. 96 (2006) 201601

